What is heat flux?

This article is a short introduction to the heat flux definition.

Heat flux, also known as thermal flux, is a term used to express an amount of energy transferred from one place to the other in the form of heat. Heat, the energy associated with the temperature of an object, travels from high temperature to low temperature. Measuring this heat flux with heat flux sensors can be useful as these measurements can tell us whether the temperature of an object will go up, down or stay the same. It also tells why and how fast the temperature change is. More on this later.

Heat flux video

Looking for an introduction to heat flux measurement? Our video explains what heat flux is and how to measure it in different environments and applications. View now!

How is heat transferred? 

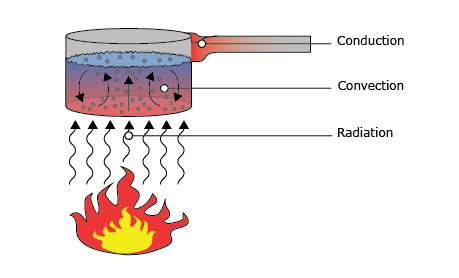
Heat can be transported by three different mechanisms. These three types of heat flux are:

1. Conduction
2. Convection
3. Radiation

These three types of heat flux combined is the total heat flux. How this relates to its temperature is easy: if the total received heat flux by an object is larger than the total heat flux going out of the object, its temperature rises. More energy enters the system than there is energy leaving and so, the energy is stored in the object as ‘heat’ leading to a higher temperature. Of course, the opposite is true as well. If the total heat flux received by an object is smaller than the total outgoing heat flux, the temperature of the object will decrease.

Let’s dive into the three parts that make up the total heat flux of an object, starting with conduction. 

Heat flux by conduction

Conduction is one of the three forms heat can flow. Heat always flows from a high temperature to a low temperature. When talking about conduction, this concerns heat flux through a solid material, (or in rare cases a non-flowing gas or liquid). When one end of a solid, let’s say the wall of a house, has a different temperature than the other end, energy is transferred. Heat starts flowing from the hot side of the wall (usually the inside of the house) to the cold side of the wall (in this case the outside). The amount of heat that flows through this wall per square meter is what we call the ‘conductive heat flux’. This is very different from the absolute temperature of the wall. The heat flux is driven by the temperature difference. 

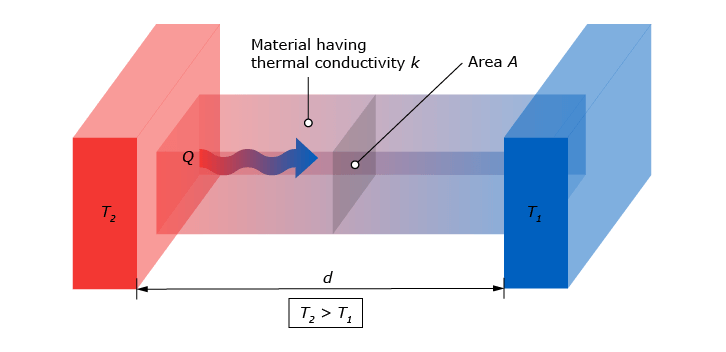
The conductive heat flux is dependent of a few factors in this particular situation:

1. The temperature ‘gradient’. This gradient is the difference between the temperature of the wall on the inside and the temperature of the wall on the outside.    
    
2. The thickness of the wall. This is the distance the heat flow has to travel through the solid. Intuitively, a thicker wall insulates better, resulting in a lower heat flow.    
    

3. The thermal conductivity of the materials of which the wall is made. Different kinds of materials conduct heat at different rates. For instance, an aluminum wall has a very high conductivity and so it will spread heat quickly. This is one of the reasons aluminum alloys are a good option for pots or pans to cook with.  

    

These three factors result in the conductive heat flux. In the following formula, (Mills, 1999), the relations of the factors are explained for a one-dimensional situation:

With:   
q(x) = Conductive heat flux per unit of area at place x. [W/m²]   
λ = thermal conductivity of material. [W/mK]   
= T₂ – T₁. Difference between temperatures at place x₁ and x₂. [K]   
= x₂ – x₁. Distance between location of T₁ and T₂. [m]   

The first thing to explain is the unit of q(x), W/m². The ‘W’ represents Watts, a measurement of Joules per second. Furthermore q(x) is expressed per square meter ‘m²’. This means that, to attain the total heat flowing through the wall, we must account for the length and height of that particular wall. 

The term is called the temperature gradient. We are looking for the heat flux between two sides of a wall, a cold side and a hot side. The distance between these sides, or the thickness of the wall, is . The difference of temperatures of the hot and cold side is . When divided, we attain the temperature gradient. This gradient dictates which way the heat flows and partially how fast it flows. 

The minus-sign in front of the expression indicates the heat flux direction: heat always flows from a high temperature to a low temperature, and because = T₂ – T₁, this term will also always be negative as T₁  > T₂. To correct for this, another minus-sign creates a positive heat flux. 

Conductive heat flux is everywhere around us, continuously. Every solid material touching another solid material with a different temperature is interchanging heat. Usually in much more complex forms and shapes than just a wall.    

We’re heating up, onto the next!

Heat flux by convection

As before, convection is one of the three ingredients determining the total heat flux of an object. What characterizes convection is that it is transferred by a fluid or gas. This fluid can be either a liquid or a gas. This phenomenon can be separated into two kinds: natural convection and forced convection. 

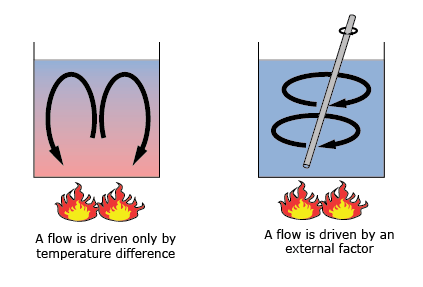
The first one, natural convection, occurs when fluids or gasses heat up or cool down. With their temperature, their volume and thus density change. This leads to an often circular motion in a system. A fluid or gas heats up, expands, floats up, cools down, shrinks, sinks and heats up again. For instance, think about the oceanic currents, wind currents or hot air rising above a fire.

Forced convection is a process in which gasses or fluids are deliberately put in motion. This may be convection induced by a power source such as an air conditioner, pumps, fans, boilers, using your oven or boiling a pot of water.

Both types have slightly different physics. Before doing any measurements and calculations it is useful to establish with what type of convection you are dealing.

Furthermore, we can make a distinction between internal and external convection. Internal convection concerns systems with the fluid or gas at the center like oil pipes. External convection on the other hand, regards the fluid or gas on the outside like air around a hot car in traffic.

The last big distinction to be made is the type of flow regarding the fluid. One can imagine that a very busy river spreads heat differently than water flowing at a constant speed through a tube. Different situations have different amount of mixing of the fluid. The more mixing that occurs, the more heat flux develops in and around the fluid. This property is called ‘turbulence’. The wilder the fluid or gas behaves, the more turbulent the system is, thus the higher the heat flux will be. This turbulence is expressed with the ‘Reynolds number’. The Reynolds number of a fluid or gas depends on its density, speed, geometry and viscosity. 

With enough experimenting, research and numerical models, the following expression was found for convective heat flux, (Mills, 1999): 

With:   
q = Convective heat flux per unit of area. [W/m²]   
h_c = convective heat transfer coefficient; A constant for rate of convection, different for every particular system. [W/m²K]   
= The difference in temperature of the solid and the fluid. [K]

The most difficult factor regarding convective heat flux is always the measuring or calculating of the heat transfer coefficient h_c. This variable is dependent on temperature, geometry of the system, velocity of the fluid or gas, dimensions of the solid, viscosity, densities and much more.

Typical heat transfer coefficients for air are: 

• 2.5 ∼ 25 W/m²K for natural convection
• 10 ∼ 500 W/m²K for forced convection

Typical heat transfer coefficient for water are:

• 50 ∼ 3,000 W/m²K for natural convection
• 50 ∼ 10,000 W/m²K for forced convection
• 2,500∼ 25,000 W/m²K for boiling water
• 5,000 ∼ 100,000 W/m²K for condensing water vapor

The last form of heat flux we will talk about is one you have probably already heard of; Radiation. 

Heat flux by radiation

Even though most people do not realize it, almost all objects emit at least some radiation. Radiation is energy in the form of an ‘electromagnetic radiation’. This might sound strange, but in reality it is just light, although often not the visible type. Electromagnetic radiation is energy emitted by a radiator and absorbed or reflected by another body. All the light that we can see, the visual spectrum, is only a fraction of the light that is emitted around us. For now, we will only do a short explanation on light. All forms of light, or electromagnetic radiation, have a frequency. This frequency tells us how much energy exactly is present in one quantum of light. A quantum of high frequency has more energy inside them than a low frequency quantum. 

For instance: UV-radiation, emitted by the sun, carries a lot of energy with it per quantum. So much so, that it can bump into molecules of your skin and alter the charge of the molecule, irritating your skin and leaving you burned. On the other hand, infrared radiation is also emitted by the sun, carrying relatively less energy per quantum. This, more tame, quantum bumps into your molecules with no other effect than vibrating them a bit, not capable of knocking electrons out of orbit. This radiative heat flux has much more total energy in [W] than UV and is experienced as a heat. 

So, the sun, fire, lamps, televisions, radio signals and even people emit the same kind of energy: Radiation. Different frequencies result in different energies with different experiences and uses. The radiation most often referred to when it comes to heat flux sensors is far infrared radiation. This is longwave, invisible radiation. This radiation can be absorbed, reflected and emitted. Radiation is an interaction between two objects, often referred to as bodies.

The amount of radiation leaving body 1 and arriving at body 2 is defined by the following expression (Mills, 1999): 

With:  
= radiative heat flux from body 1 to 2. [W]  
= The transfer factor from body 1 to 2. [-]  
= The radiative surface of body 1. [m²]  
= Stefan-Boltzmann constant of 5.67 * 10^-8. [W/m²K⁴]  
T₁ = Temperature of body 1 at the surface. [K]  
T₂ = Temperature of body 2 at the surface. [K]

The transfer factor depends on both bodies. It is the relation between the sizes and shapes of the two surfaces, but is also dependent on the emissivity and absorption of bodies 1 and 2, the emitter and receiver. The emissivity of a surface represents its ease of emitting energy and is dependent of material properties like color and smoothness. Generally speaking, the transfer factor is different for every situation and can vary between 0 and 1.   

The surface area of body 1, A₁, is very straightforward. The more surface the body has, the more radiation it can emit. The Stefan-Boltzmann constant, , is independent of the situation and always has the same value. Lastly, the temperatures of both bodies influence the radiation hugely. As we can see, the temperatures are raised to the fourth power, making the radiative heat flux an extremely exponential process. In other words, at higher absolute temperatures, the same temperature difference can result in a higher exchange of radiative heat.

Having gone through all three types of heat flux, we can now put together what we have learned into a system. 

Total heat flux

With conduction, convection and radiation we can create a system and explain all heat fluxes. One thing is important to keep in mind: for now we consider a system in equilibrium. That means that, as time passes, all temperatures are constant over time. This is the case when all objects emit the same amount of energy as they receive and is one of the most common situations.